Follow @SBC_Games
This article was originally published at Gamedev.net. The discussion there, below article, brings some improvements to solver part of generator.
1. Introduction
If you ever wanted to create a puzzle
game you probably found that implementation and coding of game rules is
relatively easy, while creating the levels is a hard and long-lasting
job. Even worse, maybe you spent a lot of time on creating some levels,
with intent to incorporate specific challenges into it, but when you
asked your friend to try it, she solved it in a totally different way or
with shortcuts you never imagined before.
How great would it be if you found a way
to employ your computer, saved lot of time and solved issues similar to
the above mentioned... Here is where the procedural generation comes to
the rescue!
It is necessary to say that while there
is only one correct way how, for example, to sum vectors and every
programmer wanting to do it has to follow the same rules, when it comes
to procedural generation you are absolutely free. No way is right or
bad. The result is what counts.
2. Fruit Dating – its rules and features
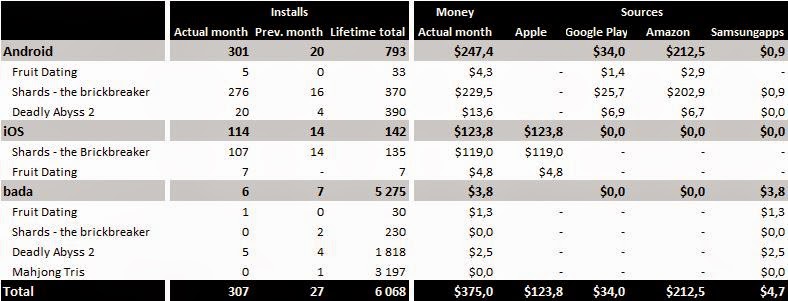
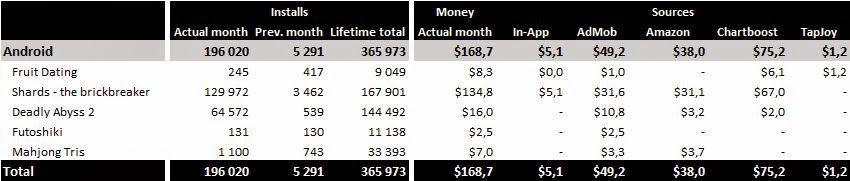
In past days we released our Fruit Dating game for iOS devices (it is also available for Android
and even for unreleased Tizen). The game is a puzzle game with simple
rules. Your target is to match pairs of fruit of the same color simply
by swiping with your finger. The finger motion matches the tilting of
the board in any given direction. So, while trying to fulfill your goal,
various obstacles like stones, cars or other fruit, get in the way.
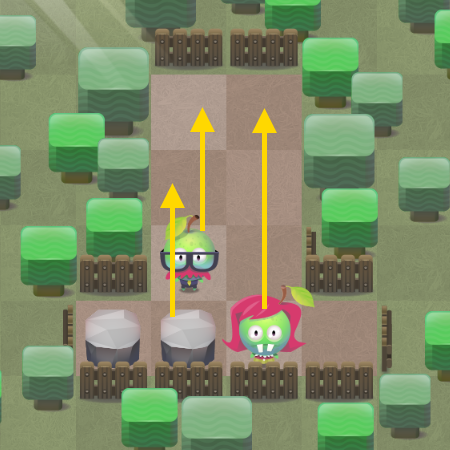
Simply, all movable objects move in the same direction at once. To
illustrate, in the pictures below you can see first level that needs 3
moves to match a pair.
Over time new features are introduced:
| One-ways are placed on the border of the tile and limits directions in which you can move. | |
| Anteaters can look in any direction, but its direction is fixed and unchanging during the level. When fruit is in the direction of the anteater and no obstacles are in the way, the anteater will shoot its tongue and drag the fruit to it. | |
| Mud can be passed through with stones, cars or barrels but not by fruit. When the fruit falls into mud it gets dirty and there is no date! | |
| Sleeping hedgehog is sitting on a tile and wakes up when hit by something. If hit by a barrel, stone or car he falls asleep again as these items are not edible. But when he is hit by fruit he eats it. |
You probably noticed that the game is
tile-based which simplifies things as each level can be represented with
a small grid. Maximum size is 8x8 tiles but as there is always solid
board, the “usable” area is 6x6 tiles. It may seem to be too small but
it proved that some very complex puzzles can be generated for it.
With the basic rules (as the additional
features were added later) I started to build my generator. My first
thought was that someone in the world surely already solved a similar
problem, so I started to search the internet for procedural generation
of levels for puzzle game. It showed that this topic is not widely
covered. I found only a few articles useful for me. Most of them were
about generating / solving Sokoban levels - for example:
It was also interesting, that most of them were written by academic
people (professors of Sokoban! :-)) From the papers I learned two
things: first, when generating something randomly it is good if it has
some symmetry in it as people will perceive it more positively. Second,
the algorithm is up to you, but none is ideal.
3. Solver
As it was obvious that every generated
level will have to be tested (whether it is possible to solve it and how
easy or hard it is) I first wanted to code a solver. As at that time I
was only considering basic rules and not features added later I came up
with these ideas for the solver:
- from initial position you can start in any direction (up, left, right, down),
- from next position you can continue in any direction again,
- in any position check for fruit match, remove matched fruits from board and continue with b) until some fruits remain on board.
As you can see, it is a simple brute
force approach. So, the number of possible board situations was: 4, 4*4 =
4^2, 4*4*4 = 4^3, … 4^n. In the 10th move it was more than a million
board situations and in the 25th move it was 1125899906842624 board
situations. Okay, you could limit maximum moves to some number, let's
say 10 and not be interested in more difficult levels, but there is
hidden another danger. Some of the puzzles can be designed or generated
in such a way that if a player does some bad moves in the beginning, she
cannot finish the level. Or, in some levels you can get into a loop of
board situations. If the algorithm branched early into such a way the
level would be marked as not solvable, even if there were other branches
with a simpler solution. Also if this algorithm found a solution there
would not be any guarantee that it is the shortest solution – you would
have to finish all branches to find the shortest solution. Beside this
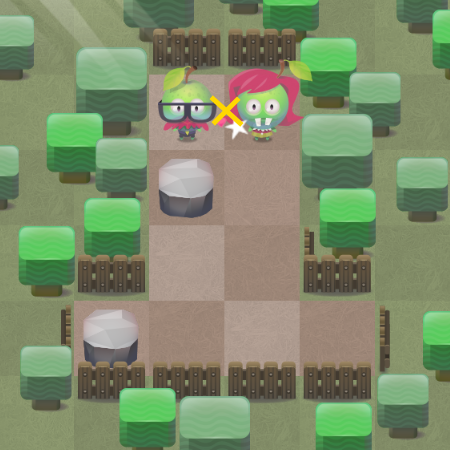
there are very often board situations in which one move in particular
direction does not change anything. See third picture in “Fruit Dating –
its rules and features” - there is no change if moved left.
So, the rules changed:
- from current position try to move in any direction,
- if there is a change in the board situation, check if the situation is new or you already were in such a situation,
- if a new situation, store it along with solution depth (number of moves to get into this situation)
- if previously was in this situation and solution depth was equal or lower, terminate this branch. Else, remove old situation (as you just got into it with less moves) and continue.
There are also other rules, like checking
matches and thus terminating the whole process when a solution is found
and later new rules when features were added, but this is the core of
the solver. It quickly cuts whole branches without a solution. Beside
solution depth, it also references to parent situations stored in each
board situation, so it is easy to print the final solution in the end.
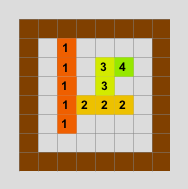
Let's show it on the first level of the game:
From the initial position a move into all
four directions is possible. These are labeled 1-1, 1-2, 1-3, 1-4. The
algorithm always tries to move right, up, left, down in this order. As
it employs a stack to store situations to examine further, the first
situation to continue is the last one pushed onto the stack (1-4 in this
case). Again, first is a move to the right (2-1) and as this is a new
situation it is put onto the stack. Next is a move up which results in
situation 2-2. We already were in this situation and it was in the first
round. So, we apply rule d) and terminate this branch – nothing is put
onto the stack. Next, a move to left is tried. It results in a new
situation (2-3) and this is put onto the stack. Last move is down, but
there is no change between 1-4 and 2-4 so we put nothing onto the stack
(rule b) … no new situation = do nothing). Now, the stack top situation
is 2-3. From it we move right and get into situation 3-1, which is equal
to situation 2-1. But in 2-1 we were in the second round so we
terminate this branch. Next we move up and fruits are on adjacent tiles,
matched and as it was the only pair the game ends.
The algorithm works, however it may not
find the shortest way. It is simply the first solution found. To
overcome this I first start with limiting the maximum moves to 30. If a
solution is not found I say that the level has no solution. If a
solution is found in, let's say, 15 moves I run the solver again with
maximum moves depth 14 (15 – 1). If no solution is found then 15 was the
shortest way. If solution is found in, let's say, 13 moves I run the
solver again with 12 (13 – 1) maximum allowed depth. I repeat while some
solution is still returned. The last returned solution is the shortest
solution.
See discussion on Gamedev.net below article. As Makers_F pointed the correct way would be to use Uniform Cost search. The algorithm described is fortunately only one step from it. When exploring new board situations, prefer those with lowest cost, where cost is number of moves to get into the situation. In other words, described algorithm in point c. is storing it into LIFO stack. Replace it with priority queue. The rule d. then changes from "if previously was in this situation and solution depth was equal or
lower, terminate this branch." to "if previously was in this situation, terminate this branch.". After these changes the algorithm will find the shortest solution in first iteration.
4. Generator
Now that the solver works, we can move to the generator and validate every generated puzzle with it.
The generation phase can be split into two parts:
- generating walls
- generating on-board objects
The wall generation always start with drawing a solid board border:
Some random parameters are generated that
say whether wall will be paint by one tile a time or two tiles a time.
If two tiles a time then random symmetry is generated. It says where the
second tile will be placed – if it will be flipped horizontally,
vertically or rotated by 90 degrees or combination of these. First grid
in the picture below is when one tile a time is painted. The rest are
for two tiles a time with different random symmetries:
The number of walls is random as well as
their length and direction. Each wall starts from a random point on the
border. Every wall is drawn in one or more iterations. After the first
iteration, a random number between 0 and wall length – 1 is chosen. If
equal to zero, the iteration loop is terminated. If greater than zero,
then this number becomes the length of the next part of this wall. A
random point on the current wall part is chosen, direction is set
randomly to be orthogonal to the current wall part and the next part of
the wall is drawn. The result may look like this (the numbers label the
iterations):
From picture it can be seen that every
next part of the wall is shorter, so you can be sure it will be
terminated at some point.
So far all walls started from the border,
so every single tile was always connected to the border. It looked
boring so I added another step where inner walls are generated. Inner
walls are not connected to any existing tile. It starts by selecting a
random tile and checking if it is free as well as its 3x3 tiles
surrounding. If yes a wall WILL be placed into the grid
and the next tile is chosen based on random direction (this direction
is randomly chosen before first tile was tested). Loop terminates when
condition for 3x3 free surrounding is not true. Notice the stress on
word “will” above. If you placed the wall into the grid immediately and
proceeded to next tile, the 3x3 surrounding would never be free as you
just placed a wall there. So I store all wall tiles into some temporary
array and place them into the grid at once when the loop is terminated.
During wall generation some of the walls
may overlap others and it is very probable that some small spaces will
be created or even that the initial area will be divided into several
disconnected areas. This is something we do not want. And this is why in
the next step I check which continuous area is largest and fill all
others with walls.
In this check I iterate through the whole
board grid and if the tile is free I recursively fill whole continuous
area with area ID (free tiles are tiles without wall and with no area ID
yet). After that I iterate through the whole board again and count
tiles for each area ID. Finally I iterate the board one last time
filling all tiles with area ID with walls except for the area ID with
the highest count.
The whole process of generating walls can
be seen in this animation. There is wall generation, inner wall
generation and in the last frame a hole in lower right corner is filled
during area consolidation:
When walls are generated we can generate
objects. We need at least one pair of fruit and zero or more obstacles
(represented by stones, cars, barrels in the game).
It would be nice if fruit was placed most
of the times into corners, in the end of corridors or so. Placing it in
the middle of an open area can be also interesting sometimes but the
first is more preferable. To achieve this we will add weights to every
free tile from the point of its attractiveness for placing fruit there.
For the end of corridors, surrounded with
tiles from 3 sides I selected weight 6 + Random(3). For tiles in
horizontal or vertical corridors I selected weight 2. For corners I
selected 3 + Random(3) and for free areas 1.
From weights it is obvious that the most
preferable placement is in the end of a corridor, followed with
placement in corners, corridors and free areas. The random numbers in
weights can also influence this and change weights between corridor ends
and corners. The weights are generated only once for each generated
level.
Obstacles (stones, cars, barrels) are
placed in a similar way, only the difference is these weights are
separate from weights for fruits and also some random obstacles density,
which says how many obstacles will be in level, is chosen.
By the way, with the weights you can do
other tricks. Features added later were sleeping hedgehog or anteater
(see features description in the beginning). Placing them into the
middle of a corridor made no sense so they have a weight for corridors =
0.
In animation bellow you can see populating level with fruits and obstacles:
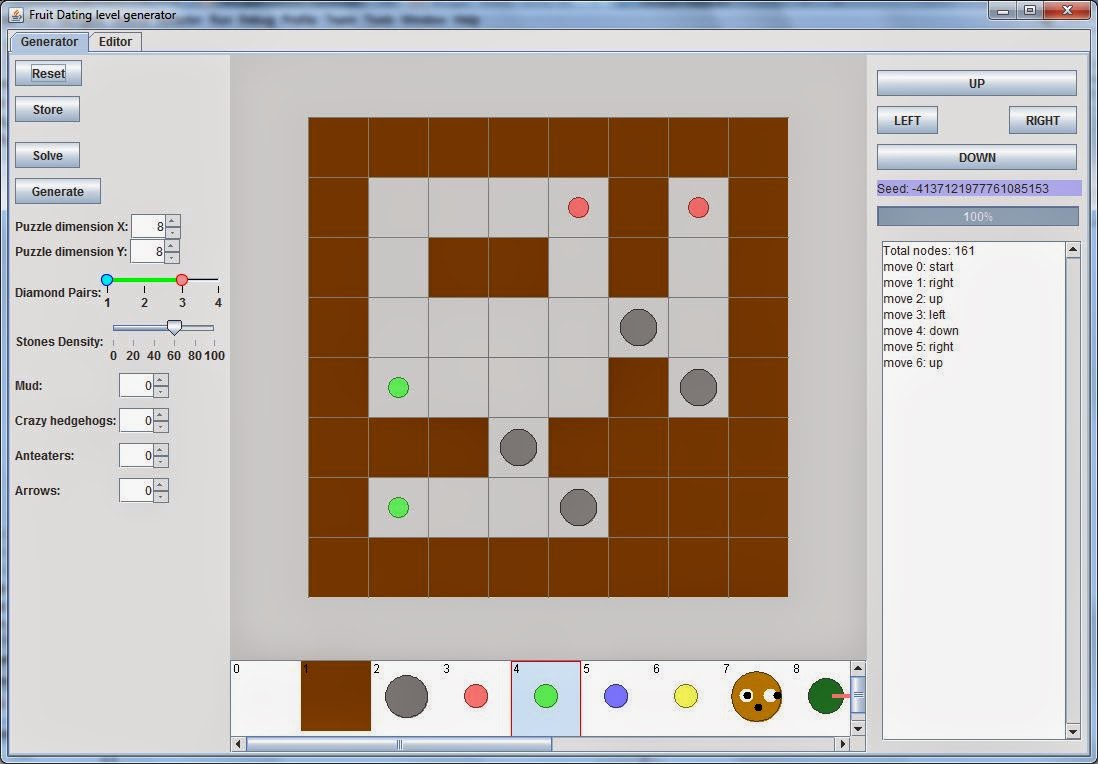
The final generated level is in the
static picture below. It takes 6 moves to solve it (right, up, left,
down, right, up). Great, after 1-2 minutes of clicking on the Generate
button we have a level that looks interesting, and the solution is
possible in 6 steps (no one will play levels with solution in 30
steps!), while it is also not a breeze to find it. But … it still could
be little bit better. It is this point where our manual entries took
place to make the levels nicer.
5. Editor
The generation ended in the previous
part. Our editor supports drag and drop, so it is easy to rearrange the
objects to achieve a higher level of symmetry like this:
It is important to re-test the level with
the solver after adjustments. Sometimes a small change may lead to an
unsolvable level. In this case the adjustments increased the number of
solution steps from six to seven.
With this manual step the approach to
procedurally generated levels forks. If you need or want manual
adjustment then procedural generation only works for you as a really big
time saver. If this step is not necessary or you think that generated
levels are OK then the generator can be part of the final game and
players have the possibility to generate future levels by themselves.
6. Final result
Generating levels procedurally saved us
enormous amounts of time. Although the generator also generates rubbish –
levels too easy to complete or levels too hard to complete, levels full
of obstacles or ugly looking levels - it still saved us an enormous
amount of time. It also allowed us to make selections and throw a lot of
levels away. If we made it by hand it would take months. This is how
levels generated in this article look like in the final game: